Dũng đang học về Quaternion, một loại số siêu phức thường được dùng để biểu diễn phép quay quanh một điểm. Để có thể hình dung các tính chất của Quaternion một cách rõ ràng hơn, anh đã tự làm rất nhiều đường tròn bằng đất sét. Trong lúc nghịch với những đường tròn đó, anh đã nghĩ ra một bài toán đơn giản không liên quan đến Quaternion như sau:

Cho một đường tròn tâm ~(s_1,s_2)~ bán kính ~r~ trên mặt phẳng tọa độ ~Oxy~. Mỗi lần biến đổi, Dũng được chọn một điểm nằm trên đường tròn, rồi xoay đường tròn quanh điểm đó một góc ~\phi~ tùy ý. Hãy viết chương trình tính xem Dũng cần ít nhất bao nhiêu lần biến đổi như vậy để biến đường tròn tâm ~(s_1,s_2)~ bán kính ~r~ thành đường tròn tâm ~(f_1,f_2)~ có cùng bán kính.

Input

• Gồm một dòng duy nhất chứa năm số nguyên ~r, s_1, s_2, f_1, f_2~ ~(1 \leq r \leq 10^5, -10^5 \leq s_1, s_2, f_1, f_2 \leq 10^5)~

Output

• Gồm một dòng duy nhất chứa một số nguyên là số lần biến đổi ít nhất để biến đường tròn tâm ~(s_1, s_2)~ thành đường tròn tâm ~(f_1,f_2)~.

Sample

Input #1

2 0 0 0 4

Output #1

1

Hint

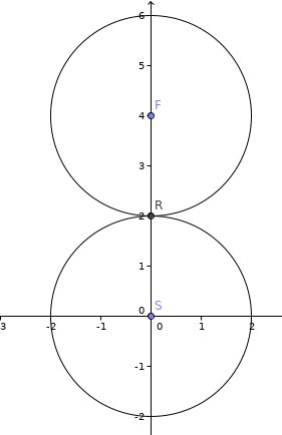
• Ta có thể biến đường tròn tâm ~(0,0)~ bán kính ~2~ thành đường tròn tâm ~(0,4)~ có cùng bán kính bằng việc thực hiện phép quay ~180~ độ quanh điểm ~(0,2)~ nằm trên đường tròn tâm ~(0,0)~ bán kính ~2~.

Problem source: Kc97ble - Free Contest