Ở Nam cực có ~N~ tảng băng được đánh số từ ~0~ tới ~N − 1~. Trên mỗi tảng băng này có một số con chim cánh cụt đang sinh sống. Mỗi tảng băng có kích thước rất nhỏ nên ta có thể coi chúng như một điểm trên hệ tọa độ. Nhân dịp đội bóng đá của Nam Cực thắng đội Bắc Cực, các con chim cánh cụt quyết định tổ chức một buổi liên hoan mừng chiến thắng. Các con chim cánh cụt quyết định chọn một tảng băng nào đó làm nơi liên hoan. Để di chuyển từ tảng băng này đến tảng băng kia, các con chim cánh cụt có thể nhảy nếu khoảng cách giữa hai tảng băng nhỏ hơn hoặc bằng ~D~. Tuy vậy, do tình hình nóng lên của Trái Đất nên các tảng băng này rất dễ tan chảy. Cứ mỗi khi có một con chim cánh cụt nhảy ra khỏi một tảng băng, tảng băng ấy lại bị giảm xuống 1 cm. Cứ như thế, khi chiều cao một tảng băng giảm xuống đúng 0 cm thì tảng băng đó sẽ chìm xuống và tan chảy luôn.

Bạn được cho vị trí các tảng băng, độ cao của các tảng băng, số ~D~ là độ dài lớn nhất mà một con chim cánh cụt có thể nhảy. Bạn hãy tính xem có thể tổ chức liên hoan ở những tảng băng nào.

Input

• Dòng đầu tiên ghi số nguyên ~N~ và số thực ~D~.
• ~N~ dòng tiếp theo, mỗi dòng ghi 4 số ~x, y, u, v. (x, y)~ là tọa độ của tảng băng, ~u~ là số con chim cánh cụt hiện đang ở trên tảng băng đó và ~v~ là độ cao của tảng băng đó.

Output

• Nếu không có tảng băng nào thỏa mãn, in ra −1.
• Nếu có tảng băng thỏa mãn, in ra danh sách các tảng băng đó theo thứ tự tăng dần.

Sample

Input #1

5 3.5
1 1 1 1
2 3 0 1
3 5 1 1
5 1 1 1
5 4 0 1

Output #1

1 2 4

Input #2

3 1.1
-1 0 5 10
0 0 3 9
2 0 1 1

Output #2

-1

Hint

Hình ảnh dưới đây giải thích cho test #1

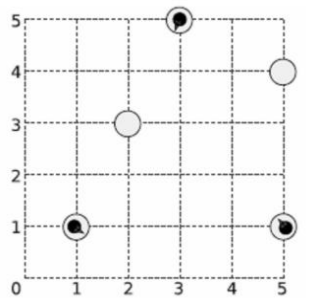
Problem source: Kc97ble - Free Contest 17