Trên một con đường biểu diễnn hư trục số thực có ~n~ mỏ vàng đánh số từ 1 tới ~n~. Mỏ thử ~i~ nằm ở tọa độ ~x_i~, có tổng trữ lượng vàng là ~g_i~, trong mỏ còn có lượng đá đủ để xây dựng đoạn kè có độ dài ~r_i~. Trong mùa mưa lũ, việc phòng chống ngập cho các mỏ trở nên cấp thiết và rất khó khăn trong việc vấn chuyển vật liệu kè. Vì vậy, chính phủ muốn dùng đá ở một dãy mỏ liên tiếp để xây dựng một đoạn kè liên tục bảo vệ tất cả các mỏ ở đó. Ta có thể coi cửa các mỏ vàng rất nhỏ, nên dù chỉ nằm ở đầu đoạn kè thì mỏ vẫn được an toàn.

Yêu cầu: Hãy giúp chính phủ xác định đoạn kè có thể xây dựng với tổng trữ lượng vàng trong các mỏ được bảo vệ là lớn nhất.

Input

• Dòng đầu tiên chứa số nguyên dương ~n~ là số lượng mỏ vàng.
• ~n~ dòng tiếp theo, dòng thứ ~i~ chứa 3 số nguyên ~x_i, g_i, r_i~ cách nhau bởi dấu cách

Giới hạn:

• ~n \le 10^5~
• ~-10^9 \le x_1 \lt x_2 \lt ... \lt x_n \le 10^9~
• ~0 \le g_i, r_i \le 10^9~

Output

• Ghi ra một số nguyên duy nhất là tổng trữ lượng vàng lớn nhất trong các mỏ được bảo vệ theo phương án tìm được.

Sample

Input #1

4
0 5 1
1 7 2
4 4 1
7 15 1

Output #1

16

Hint

Hình ảnh sau giải thích cho ví dụ trên:

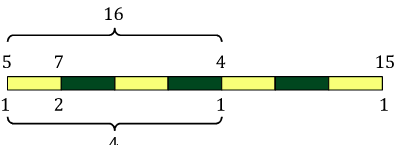
Problem source: PreVNOI Ⅴ (BẮC GIANG 2015)