HNNG - Tháp Hà Nội Ngược
Xem dạng PDFTrong bài toán Tháp Hà Nội, có ~N~ đĩa theo thứ tự từ nhỏ đến lớn đang nằm ở cột ~A~ như hình bên dưới:
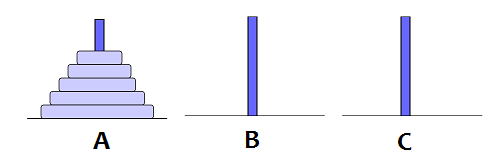
Cần chuyển ~N~ đĩa trên từ cột ~A~ sang cột ~B~ (lấy cột ~C~ làm cột trung gian) theo quy tắc:
- Mỗi lần chỉ chuyển một đĩa.
- Đĩa nhỏ phải nằm trên đĩa lớn tại bất kỳ thời điểm nào trong quá trình chuyển.
Nhưng khác với bài tháp Hà Nội cổ điển, bài tháp Hà Nội ngược này được thêm một quy tắc sau:
- Mỗi lần chỉ được chuyển 1 tầng tháp từ một cọc sang cọc sát nó theo NGƯỢC chiều kim đồng hồ:
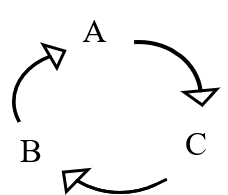
Câu hỏi như sau: Để chuyển ~N~ đĩa từ cột ~A~ sang cột ~B~ theo quy tắc trên, thì phải chuyển ít nhất bao nhiêu lần?
Input
Gồm ~1~ dòng duy nhất chứa số nguyên dương ~N~ là số đĩa ở cột ~A (1 \le N \le 10^4)~
Output
Gồm ~1~ dòng chứa duy nhất ~1~ số nguyên dương là kết quả của bài toán trên.
Đáp án cần in ra có thể rất lớn, hãy in ra đáp án sau khi chia dư cho ~10^9 + 7~
Sample
Input #1
3
Output #1
21
Input #2
2
Output #2
7
Hint
- Với #2 ta có các bước xếp đĩa sau:
~01~ ~A - C~
~02~ ~C - B~
~03~ ~A - C~
~04~ ~B - A~
~05~ ~C - B~
~06~ ~A - C~
~07~ ~C - B~
Tổng cộng có ít nhất ~7~ lần xếp.
Bình luận
hello ae