Cho hai dãy số nguyên ~a_1, a_2, …, a_n~ và ~b_1, b_2, …, b_m~ trong đó dãy số ~a_1, a_2, …, a_n~ đã được sắp xếp không giảm (tức là ~a_1 ≤ a_2 ≤ … ≤ a_n~). Với mỗi chỉ số ~i~ ~(1 ≤ i ≤ m)~ hãy tìm sự xuất hiện của ~b_i~ trong dãy ~a_1, a_2, …, a_n~.

Input

• Dòng đầu ghi hai số nguyên dương ~n~ và ~m~;
• Dòng thứ hai ghi ~n~ số nguyên ~a_1, a_2, …, a_n~;
• Dòng thứ ba ghi ~m~ số nguyên ~b_1, b_2, …, b_m~.

Hai số liên tiếp trên một dòng được ghi cách nhau một dấu cách.

Giới hạn:

• ~1 ≤ n, m ≤ 10^5; |a_i|, |b_i| ≤ 10^9~.

Output

• Một xâu nhị phân độ dài ~m~, trong đó ký tự thứ ~i~ ~(1 ≤ i ≤ m)~ là 1 nếu ~b_i~ có xuất hiện trong dãy ~a_1, a_2, …, a_n~, và là 0 nếu ngược lại.

Sample

Input #1

7 5
1 2 3 4 4 6 7
3 1 5 4 8

Output #1

11010

Problem source: Chuyên Sơn La Online Judge

Cho hai dãy số nguyên ~a_1, a_2, …, a_n~ và ~b_1, b_2, …, b_m~ trong đó dãy số ~a_1, a_2, …, a_n~ đã được sắp xếp không giảm (tức là ~a_1 ≤ a_2 ≤ … ≤ a_n~). Với mỗi chỉ số ~i~ ~(1 ≤ i ≤ m)~ hãy tìm sự xuất hiện của ~b_i~ trong dãy ~a_1, a_2, …, a_n~.

Input

• Dòng đầu ghi hai số nguyên dương ~n~ và ~m~;
• Dòng thứ hai ghi ~n~ số nguyên ~a_1, a_2, …, a_n~;
• Dòng thứ ba ghi ~m~ số nguyên ~b_1, b_2, …, b_m~.

Hai số liên tiếp trên một dòng được ghi cách nhau một dấu cách.

Giới hạn:

• ~1 ≤ n, m ≤ 10^5; |a_i|, |b_i| ≤ 10^9~.

Output

• Một dòng duy nhất chứa ~m~ số nguyên, trong đó số thứ ~i~ ~(1 ≤ i ≤ m)~ là chỉ số ~j~ nhỏ nhất mà ~a_j = b_i~ (nếu tồn tại) và là ~0~ nếu ngược lại. Hai số liên tiếp được ghi cách nhau một dấu cách.

Sample

Input #1

7 5
1 2 3 4 4 6 7
3 1 5 4 8

Output #1

3 1 0 4 0

Problem source: Chuyên Sơn La Online Judge

Cho hai dãy số nguyên ~a_1, a_2, …, a_n~ và ~b_1, b_2, …, b_m~. Với mỗi chỉ số ~i~ ~(1 ≤ i ≤ m)~ hãy tìm sự xuất hiện của ~b_i~ trong dãy ~a_1, a_2, …, a_n~.

Input

• Dòng đầu ghi hai số nguyên dương ~n~ và ~m~;
• Dòng thứ hai ghi ~n~ số nguyên ~a_1, a_2, …, a_n~;
• Dòng thứ ba ghi ~m~ số nguyên ~b_1, b_2, …, b_m~.

Hai số liên tiếp trên một dòng được ghi cách nhau một dấu cách.

Giới hạn:

• ~1 ≤ n, m ≤ 10^5; |a_i|, |b_i| ≤ 10^9~.

Output

• Một dòng duy nhất chứa m số nguyên, trong đó số thứ ~i~ ~(1 ≤ i ≤ m)~ là chỉ số ~j~ nhỏ nhất mà ~a_j = b_i~ (nếu tồn tại) và là ~0~ nếu ngược lại. Hai số liên tiếp được ghi cách nhau một dấu cách.

Sample

Input #1

7 5
6 4 7 2 4 1 3
3 1 5 4 8

Output #1

7 6 0 2 0

Problem source: Chuyên Sơn La Online Judge

Một hồ chứa lớn được xây dựng trên sông Hồng bằng cách sử dụng một con đập. Giả sử rằng hồ chứa là một hình hộp chữ nhật có kích thước (tính bằng đơn vị). Hồ chứa gồm nhiều bể. Hình ảnh dưới đây là một ví dụvề mặt cắt ngang của một hồ chứa rỗng theo kích thước chiều dài và chiều cao của nó:

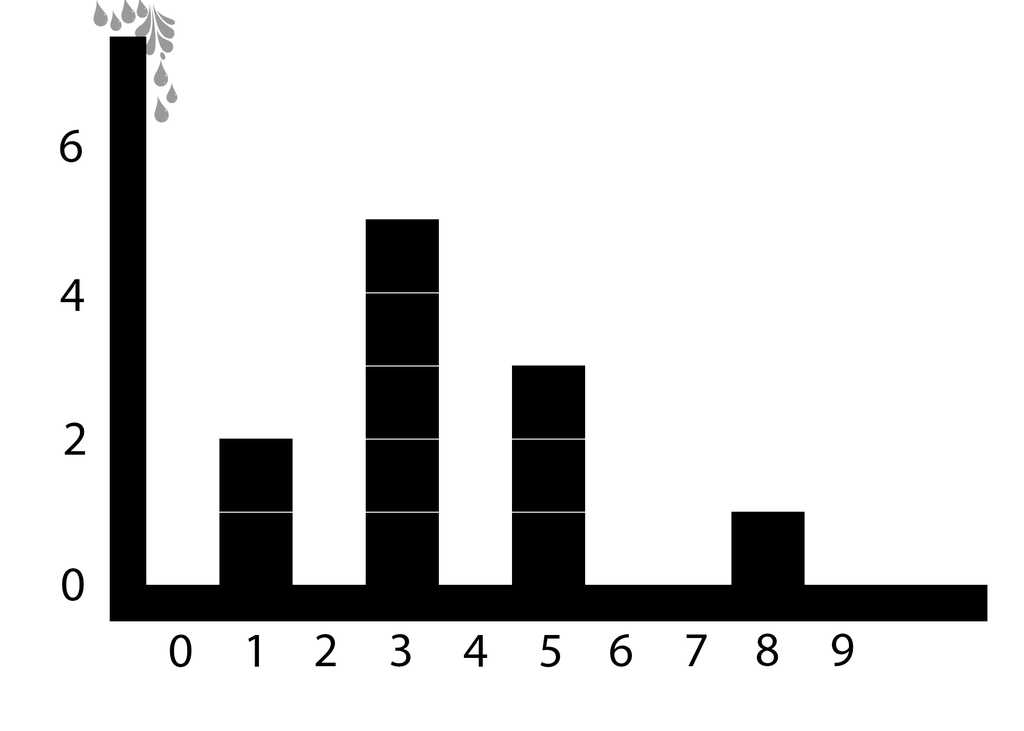
Nước chảy vào từ cửa trên cùng bên trái vào hồ chứa. Các bể chứa trong hồ được xây dựng bằng tường. Mỗi bức tường dày một đơn vị (chiều rộng) và ngắn hơn chiều cao của hồ chứa.

Cho biết vị trí và chiều cao của các bức tường và đơn vị và thể tích ~K~ của nước chảy vào, nhiệm vụ của bạn là tìm ra bức tường cuối cùng mà nước chảy tràn qua.

Input

Đầu vào bao gồm một số tập dữ liệu. Dòng đầu tiên của đầu vào chứa số lượng tập dữ liệu, là một số dương và không lớn hơn 20. Các dòng sau mô tả các tập dữ liệu.

Mỗi tập dữ liệu được mô tả bằng các dòng sau:

• Dòng đầu tiên là 1 số nguyên dương ~N~ - số lượng các bức tường ngăn cách các bể (~N \le 10^5~)
• Dòng thứ 2 chứa ~N~ số nguyên dương ~L_i~ -vị trí nằm ngang (dọc theo kích thước chiều dài của hồ chứa) của bức tường thứ ~i (1 \le L_i \le 10^9, L_i \gt L_{i-1} + 1\ \forall{i} > 1)~.
• Dòng thứ 3 chứa ~N~ số nguyên dương ~H_i~ - chiều cao của bức tường thứ ~i (1 \le H_i \le 10^5)~.
• Dòng thứ tư là một số nguyên ~Q (1 \le Q \le 10^5)~.
• Tại ~Q~ dòng tiếp theo, mỗi dòng là một số nguyên dương ~K~ cho biết thể tích nước chảy vào trong hồ chứa (~1 \le K \le 10^{15}~).

Giới hạn:

• 50% bộ test có ~T \le 10, N \le 1000, Q \le 1000~.
• 30% bộ test có ~T \le 20, N \le 10000, Q \le 10000~.
• 20% bộ test không có ràng buộc gì thêm.

Output

Với mỗi tập dữ liệu, in ra ~Q~ dòng tương ứng ~Q~ truy vấn. Dòng thứ ~i~ trả lời truy vấn thứ ~i~ là chỉ số của bức tường cuối cùng mà nước chảy tràn qua. Nếu nước không chảy tràn qua bức tường nào, in ra ~0~.

Sample

Input #1

1
4
1 3 5 8
2 5 3 1
3
3
13
17

Output #1

1
1
3

Hint

Hình ảnh dưới đây giải thích cho dữ liệu mẫu phía trên.

Problem source: ACM ICPC Asia Nha Trang Regional Contest 2016

Cho dãy số nguyên ~a~ có ~N~ phần tử ~a_1, a_2, ..., a_n~. Và ~q~ truy vấn có dạng:

• ~k~: tìm ~i~ nhỏ nhất sao cho ~a_i~ ≤ ~k~.

Input

• Dòng đầu tiên là số nguyên dương ~N~ (~1 <=N <=10^6~)
• Dòng thứ 2 là ~N~ số nguyên ~a_i (1 \le i \le N, |a_i| \le 10^6)~.
• Dòng thứ 3 là số nguyên dương ~q (1 \le q \le 10^5)~.
• ~q~ dòng tiếp theo, mỗi dòng là 1 số nguyên ~k (|k| \le 10^6)~.

Dữ liệu đảm bảo luôn tồn tại đáp số thoả mãn yêu cầu

Output

• ~q~ dòng: với mỗi dòng là kết quả của truy vấn tương ứng

Sample

Input #1

8
18 15 9 4 -3 2 8 9
4
4
9
15
2

Output #1

4
3
2
5

Hint

50% số test của đề bài có ~N~ ≤ ~1000~ và ~q~ ≤ ~1000~

Problem source: bvquoc

Cho một mảng ~a~ gồm ~n~ số nguyên dương được sắp xếp không giảm, và một mảng ~b~ gồm ~m~ số nguyên dương (có thể không được sắp xếp).

Cho biết ~f(i)~ (~1 \le i \le m~) là vị trí tương ứng của phần tử ~b_i~ trên mảng ~a~ (số thứ tự trên các mảng đều đếm từ ~1~, nếu ~b_i~ không xuất hiện ở ~a~ thì ~f(i) = -1~, nếu ~b_i~ xuất hiện nhiều lần trên ~a~ thì lấy số thứ tự nhỏ nhất).

Đặt ~X = \sum_{i=1}^{m} f(i) \mod 30~, yêu cầu của chúng ta là tính ~\lfloor 2^X \rfloor~.

Input

• Dòng đầu tiên gồm số nguyên dương ~n~ là kích thước mảng ~a~ (~1 \le n \le 10^5~).
• Dòng thứ hai gồm ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~ (~0 \le a_1 \le a_2 \le \ldots \le a_n \le 10^9~).
• Dòng thứ ba gồm số nguyên dương ~m~ là kích thước mảng ~b~ (~1 \le m \le 10^5~).
• Dòng thứ tư gồm ~m~ số nguyên dương ~b_1, b_2, \ldots, b_m~ (~0 \le b_i \le 10^9~).

Output

In ra một số nguyên duy nhất là kết quả tìm được.

Sample

Input #1

6
1 5 6 7 9 44
2
5 6

Output #1

32

Input #2

7
1 2 55 487 489 665 687
3
687 666 489

Output #2

2048

Hint

• Giải thích test 1: ~5~ là ở vị trí số ~2~ nên ~f(1) = 2~, ~6~ là vị trí số ~3~ nên ~f(2) = 3~. -> kết quả là ~2^{2+3} = 32~.
• Giải thích test 2: ~687~ ở vị trí ~7~ nên ~f(1) = 7~, ~666~ không có nên ~f(2) = -1~, ~489~ ở vị trí ~5~ nên ~f(3) = 5~. -> kết quả là ~2^{7-1+5} = 2048~.

Problem source: CLB Lập Trình PTIT

Một nhà máy sản xuất gốm sứ có hai phân xưởng. Phân xưởng nặn và phân xưởng vẽ. Đầu tiên tất cả các sản phẩm được hình thành từ phân xưởng nặn sau đó nó được chuyển sang phân xưởng vẽ để vẽ các hoa văn lên sản phẩm trước khi nung. Do hai phân xưởng này ở cách xa nhau nên trong một ngày tất cả đồ gốm sản xuất trong ngày chỉ được vận chuyển một lần duy nhất từ phân xưởng nặn sang phân xưởng vẽ bằng một ô tô chuyên dụng. May mắn là nó chạy rất nhanh nên thời gian vận chuyển xem như bằng ~0~. Sau khi hoàn thành vẽ xong, toàn bộ sản phẩm sẽ ngay lập tức đem đi nung (khi đó phân xưởng nặn sẽ ngồi chơi, phân xưởng nung làm việc).

Phân xưởng nặn có ~N~ thợ thủ công, thợ thủ công thứ ~i~ nặn một sản phẩm mất ~a_i~ đơn vị thời gian. Phân xưởng vẽ có ~M~ thợ thủ công, thợ thủ công thứ ~j~ hoàn thành vẽ hoa văn lên một sản phẩm mất ~b_i~ đơn vị thời gian.

Ngày làm việc kéo dài ~T~ đơn vị thời gian và khi bắt đầu cả trong phân xưởng nặn và vẽ không có sản phẩm nào. Ngoài ra, sau khi kết thúc ngày làm việc trong cả hai phân xưởng này cũng không còn sản phẩm nào (tức là tất cả các sản phẩm đã hoàn thành cả hai phần việc nặn và vẽ).

Hỏi rằng số lượng sản phẩm tối đa mà hai phân xưởng sản xuất trong ngày là bao nhiêu?

Input

• Dòng đầu tiên ghi số nguyên dương ~T~ ~(1 ≤ T ≤ 10^9)~;
• Dòng thứ hai ghi số nguyên dương ~N~ ~(1 ≤ N ≤ 100000)~;
• Dòng thứ ba ghi ~N~ số nguyên dương ~a_1, a_2, ..., a_N\ (a_i ≤ 10^9)~;
• Dòng thứ tư ghi số nguyên dương ~M\ (1 ≤ M ≤ 100000)~;
• Dòng thứ năm ghi ~M~ số nguyên dương ~b_1, b_2, ..., b_m\ (b_j ≤ 10^9)~.

Giới hạn:

• ~50\%~ số điểm có ~T ≤ 1000, N, M ≤ 100~.

Output

• Một số nguyên duy nhất là số lượng sản phẩm tối đa có thể hoàn thành trong ngày của hai phân xưởng.

Sample

Input #1

20
2
4 6
3
2 3 5

Output #1

5

Problem source: Kc97ble - Free Contest

Bi là một học sinh giỏi trong lớp. Sắp tới, Bi phải thi để nhận chứng chỉ cho ~M~ môn học trong vòng ~N~ ngày. Mỗi môn học được đánh số từ 1 đến ~M~ và để nhận được chứng chỉ thứ ~i~ thì cần bỏra ~t_i~ ngày để ôn tập và các ngày ôn tập không cần liên tiếp. Một ngày Bi có thể tham gia thi, ôntập hoặc nghỉ ngơi.

Bạn được biết lịch tổ chức các kì thi của ~M~ môn học sắp tới trong vòng ~N~ ngày. Hãy giúp Bi lênlịch sao cho số ngày cần là ít nhất để có thể lấy được ~M~ chứng chỉ.

Input

• Dòng đầu tiên gồm 2 số nguyên ~N, M (1 ≤ N, M ≤ 10^5).~
• Dòng tiếp theo gồm ~N~ số nguyên ~X_1, X_2, ..., X_N~ , với ~X_i (0 ≤ Xi ≤ M)~ thể hiện cho ngày thứ ~i~ có kì thi để lấy chứng chỉ ~X_i~. Nếu ~X_i = 0~ thì ngày đó không có kì thi nào được tổ chức.
• Dòng cuối cùng là ~M~ số nguyên ~t_1, t_2, ..., t_M~, với ~t_i (1 ≤ ti ≤ 10^5)~ là số ngày cần ôn tập để lấy được chứng chỉ thứ ~i~.

Output

• Gồm 1 số duy nhất là số ngày ít nhất để Bi có thể nhận được tất cả các chứng chỉ.
• Nếu không thể lấy trong vòng ~N~ ngày thì xuất -1.

Sample

Input #1

9 2
1 1 2 0 1 2 1 1 2
2 1

Output #1

5

Hint

• Bi sẽ ôn tập ngày 1 cho môn thứ 2 và thi nó vào ngày thứ 3
• Bi sẽ ôn tập ngày 2 và 4 cho môn thứ 1 và thi nó vào ngày thứ 5

Problem source: Kc97ble - Free Contest

Trên một hệ trục tọa độ Ox, có N đoạn thẳng. Các đoạn thẳng được đánh số từ 1 đến N. Đoạn thẳng thứ i có đầu mút bên trái tại Li và đầu mút bên phải tại Ri.Ta nói rằng, một điểm có tọa độ x được phủ bởi đoạn thẳng i khi và chỉ khi x nằm giữa hai đầu mút của i (tức là Li ≤ x ≤ Ri).Có Q truy vấn, mỗi truy vấn được mô tả bởi hai số nguyên a và b, yêu cầu:

• Trong số N đoạn thẳng đã cho, cần chọn ra một số đoạn thẳng, sao cho tất cả các điểm cótọa độ từ a đến b đều được bao phủ bởi ít nhất một đoạn thẳng trong các đoạn thẳng được lựa chọn. Hãy in ra số lượng đoạn thẳng ít nhất cần lựa chọn.

Yêu cầu: Viết chương trình trả lời Q truy vấn trên.

Input

• Dòng đầu tiên gồm số nguyên N (1 ≤ N ≤ 200000) - số đoạn thẳng.

• N dòng tiếp theo, dòng thứ i gồm hai số nguyên Li và Ri (~ 0 ≤ Li ≤ Ri ≤ 10^9 ~) - tọa độ hai đầu mút của đoạn thẳng thứ i.

• Dòng tiếp theo gồm số nguyên Q (1 ≤ Q ≤ 200000) - số truy vấn cần xử lí.

• Q dòng tiếp theo, mỗi dòng gồm hai số nguyên a và b (~ 0 ≤ a ≤ b ≤ 10^9 ~) mô tả một truy vấn.

Output

• Với mỗi truy vấn, in ra một dòng gồm một số nguyên duy nhất là số đoạn thẳng ít nhất cần lựa chọn. Trong trường hợp không có cách chọn, hãy in ra -1.

Sample

Input #1

5
0 3
1 2
2 4
8 10
5 8
4
1 4
0 10
8 11
5 7

Output #1

2
4
-1
1

Hint

• Với truy vấn thứ nhất, có thể chọn các đoạn thẳng 2 và 3.

• Với truy vấn thứ hai, có thể chọn các đoạn thẳng 1, 3, 4 và 5.

• Với truy vấn thứ tư, có thể chọn đoạn thẳng 5.

Problem source: Free Contest Cup 2018

Cho n số nguyên dương a1, a2,..., an. Tính giá trị lớn nhất của a[x] % a[y] với 1≤ x, y≤ n và a[y]≤ a[x].

Dữ liệu đảm bảo Maxa : Mina≤ 200000.

Input

• Dòng đầu tiên gồm 1 số nguyên n (1≤ n≤ 2e5)

• Dòng thứ hai gồm n số nguyên dương a[i] (1≤ a[i]≤ 1e6)

Output

1 số duy nhất là kết quả bài toán

Sample

Input #1

3
3 4 5

Output #1

2